La progettazione con le NTC 2018 risulta condizionata dalla modifica del criterio per stabilire se la struttura è deformabile torsionalmente. Questa condizione viene controllata mediante il rapporto r2 / Ls2, il cui valore limite rispetto alle NTC 2008 anziché essere pari a 0.8 deve essere pari almeno ad 1.0 (§7.4.3.1) per evitare che il comportamento sia deformabile torsionalmente. Con questa modifica diverse strutture che non risultavano deformabili torsionalmente potrebbero risultare classificate con questo tipo di comportamento.
Il comportamento strutturale di tipo “deformabile torsionalmente” impatta in maniera rilevante sul valore del fattore di comportamento che passa da valori medi pari a circa 3.0 a valori nell’intorno di 1.5, in funzione del parametro α0 legato alla snellezza delle pareti duttili. Il parametro r (raggio torsionale delle rigidezze) si calcola mediante la seguente formula:
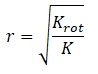Il parametro Ls è il raggio giratore delle masse (rapporto tra inerzia polare delle masse e massa totale) e può essere calcolato secondo due diversi approcci: con una distribuzione “discretizzata” delle masse secondo le indicazioni riportate nell’Eurocodice 8, o mediante una distribuzione “continua” delle masse. Il primo approccio è più nell’ottica degli elementi finiti, in quanto per forme strutturali generiche è possibile definire la massa concentrata nei nodi del modello di calcolo. La formula descritta nell’EC8 è la seguente:
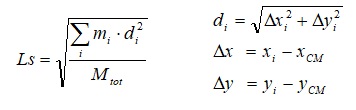Il secondo approccio è il più complicato in quanto data la generalità delle strutture l’integrazione della massa è un operazione spesso più difficile. La formula di Ls riportata nelle NTC vale per impalcati a pianta rettangolare, per le quali è possibile calcolare Ls dalle dimensioni L e B della pianta, nell’ipotesi di distribuzione uniforme della massa (centro di massa coincidente con il centro dell’ingombro):
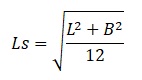Il metodo di classificazione delle strutture deformabili torsionalmente riportato nelle norme è pensato principalmente per conformazioni di edifici a piani ed impalcati essenzialmente con un comportamento rigido nel piano e massa uniforme. Un metodo più generico per classificare la struttura utilizza i modi di vibrare calcolati mediante una analisi dinamica modale. Questo metodo mette a confronto la frequenza di vibrazione del modo torsionale disaccoppiato (ωrot) con le frequenze dei modi traslazionali puri (ω) . Se il rapporto Ω è maggiore di 1 la risposta è principalmente traslazionale, se è minore di 1 la risposta è dominata da un comportamento torsionale:
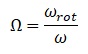Per controllare Il tipo di comportamento è fondamentale la distribuzione degli elementi strutturali primari verticali. Nell’esempio che riportiamo la struttura da un primo controllo (“ad occhio”) sembra avere comportamento prevalentemente traslazionale. A conti fatti, però, applicando le limitazioni delle NTC 2018 per r2 / Ls2 ci ritroviamo valori inferiori all’unità.
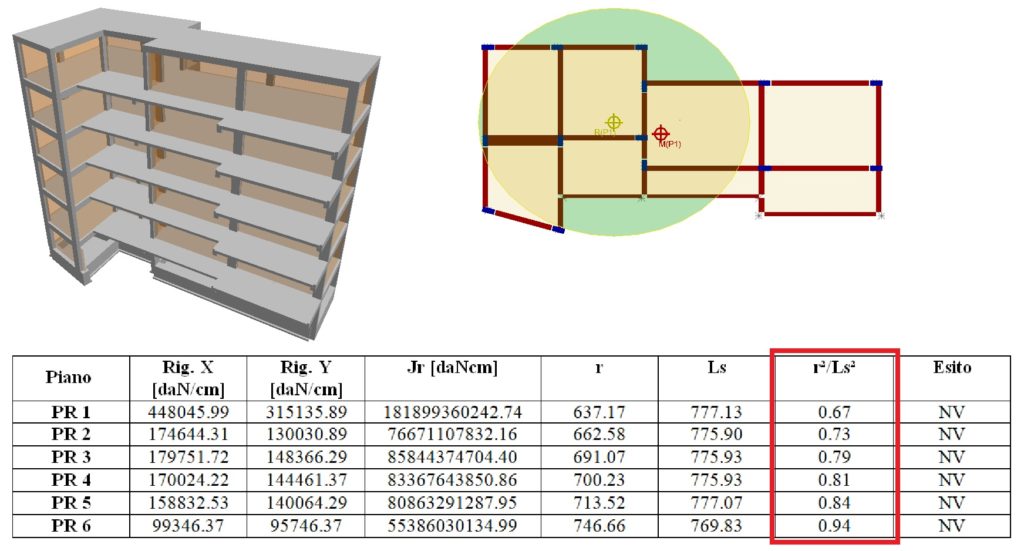
Figura 1 : Esempio di struttura deformabile torsionalmente
Come possiamo notare dalla Figura 1 i baricentri risultano evidentemente spostati verso il lato rigido della costruzione causando possibili torsioni della struttura attorno all’asse verticale. In questo caso la soluzione è risultata semplice: basta ruotare i due pilastri sulla parte destra dell’edificio in modo da avere maggiore rigidezza lungo la direzione Y (vedi Figura 2). Così facendo otterremo un comportamento molto diverso (r2 / Ls2 maggiore di 1 a tutti i livelli). Come è noto la regolarizzazione dell’ellisse delle rigidezze e l’avvicinamento dei baricentro al centro di ingombro della pianta sono obiettivi da perseguire che portano sicuramente effetti positivi.
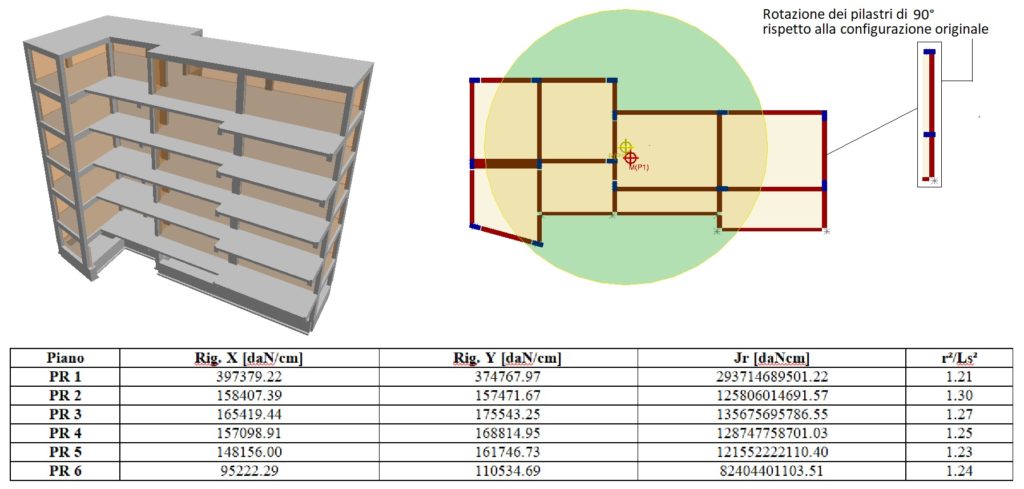
Figura 2 : Ottimizzazione delle distribuzione delle rigidezze
Per questo esempio applicando la regola delle frequenze dei modi di vibrare principali si ottiene un risultato contrastante: già la struttura originale non presenterebbe il comportamento deformabile torsionalmente. Analizzando i modi di vibrare si ottengono i seguenti risultati:
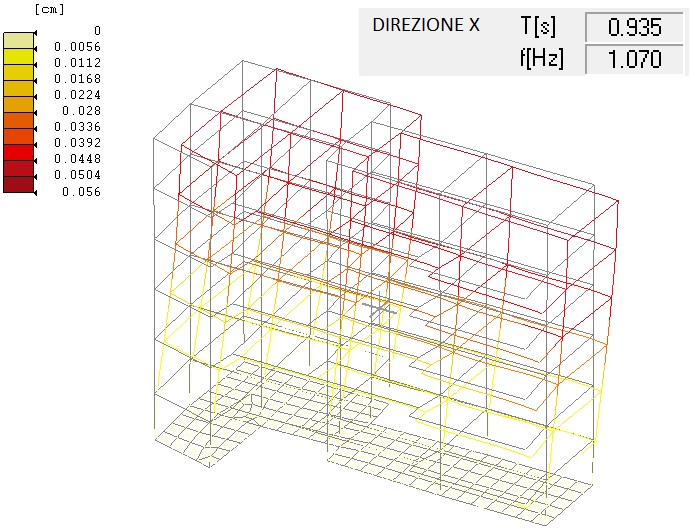
Figura 3 : Modo di vibrare fondamentale in direzione X
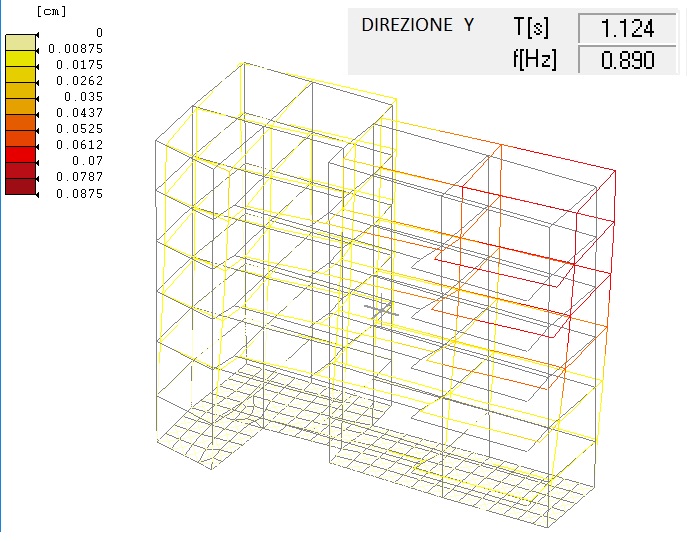
Figura 4 : Modo di vibrare fondamentale in direzione Y
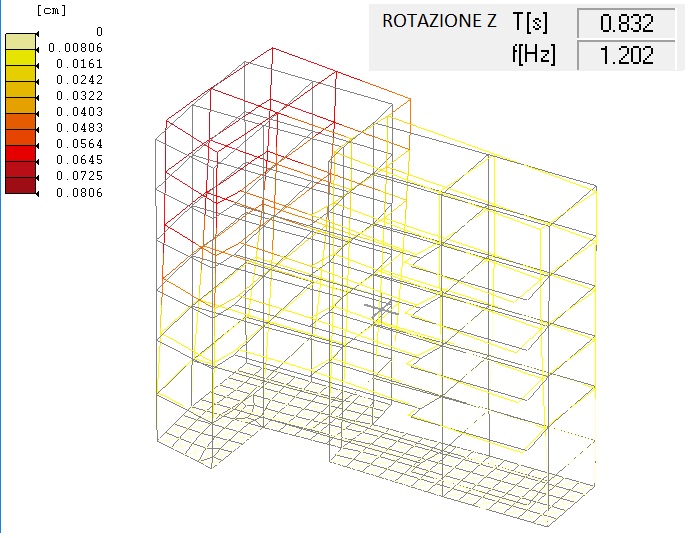
Figura 5 : Modo di vibrare torsionale predominante
Il valore minimo del coefficiente Ω è quello in direzione X, caratterizzata da una frequenza più alta del modo fondamentale:
Ωx = 1.202 / 1.070 = 1.124 > 1 (comportamento traslazionale)
Ωy = 1.202 / 0.890 = 1.350 > 1 (comportamento traslazionale)
La particolarità di questa struttura è però dovuta al fatto che l’elevata eccentricità in direzione X fa si che non ci sia un modo puramente traslazionale in direzione Y, in quanto per il modo Y e per quello torsionale (Rot Z) i fattori di partecipazione delle masse Gy e GrotZ presentano valori comparabili:
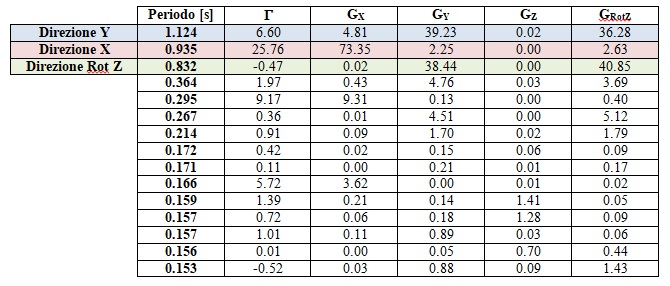
Figura 6 : Riepilogo dei modi di vibrare
La discriminante numerica in questo caso può far si che in realtà la definizione dei modi venga invertita: la scelta del modo traslazionale lungo Y è stata fatta su piccole differenze di fattore di partecipazione (39.23 contro 36.28 e 38.44 contro 40.85). Questi aspetti, in questo caso, fanno sì che, nonostante i valori numerici, la struttura potrebbe presentare un comportamento “deformabile torsionalmente”.
Alla luce dell’esempio fatto abbiamo potuto evidenziare i limiti di entrambi i metodi. Il calcolo del rapporto r2 / Ls2 da buoni risultati per edifici multipiano ad impalcato rigido. I limiti di applicabilità sono legati al fatto che il metodo si applica alla struttura scomposta nei vari livelli. Il calcolo del rapporto Ω invece è tanto più affidabile tanto più i modi traslazionali sono disaccoppiati e “lontani” da quello rotazionale. Viste le incertezze, in ogni caso sarebbe opportuno progettare con valori dei rapporti abbastanza maggiori di 1.
In definitiva abbiamo visto che la classificazione del comportamento di una struttura deformabile torsionalmente è un aspetto che difficilmente può essere “inscatolato” in formule da applicare. Come tanti altri aspetti dell’Ingegneria strutturale l’apporto della conoscenza è fondamentale ancor più delle norme.
Bibliografia:
Norme tecniche per le Costruzioni – NTC 2018
Torsional effects and regularity conditions in RC buildings – E. Cosenza, G. Manfredi, R. Realfonzo
Software utilizzato:
FaTA-e – Stacec
Volevo chiedere come mai è stata inserita la notazione omega = wrot/w dove wtor è il periodo del modo rotazionale disaccoppiato. Nella Circolare alle NTC18 l’espressione è omega = T/Trot, ossia l’inverso di quella scritta, quindi nello specifico anche con questo metodo la struttura (come per il primo caso verifica da NTC18) risulterebbe deformabile torsionalmente.
Si fa forse riferimento a qualche altra normativa?
La relazione è analoga in quanto T=2pigreco/w, quindi periodo e frequenza sono in rapporto inverso.